"JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6 - Hallo sahabat Chord Gitar Indonesia, Pada sharing Kunci gitar kali ini yang berjudul "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6, saya telah menyediakan lirik lagu lengkap dengan kord gitarnya dari awal lagi sampai akhir lagu. mudah-mudahan isi postingan kunci gitar yang saya tulis ini dapat anda pahami. okelah, ini dia chord gitarnya.

Penyanyi : "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6
Judul lagu : "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6

"JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6

Hai semua :-)

     kali ini kak Zainal akan membagikan sedikit ilmu untuk kalian yang sedang duduk dibangku Kelas 5 SD .... semoga kalian dapat menjadi smart (cerdas) setalah membaca artikel ini

ok langsung saja

Hai !!! sobat belajar 

         kali ini saya akan shere cuplikan hasil belajar saya SEMOGA BERMANFAAT YA....pada kesempatan 

ini saya mengeSHERE ilmu Matematika yaitu ilmu yang membutuhkan KETELITIAN danKETELATENAN dan yang gak kalah pentingnya dalam mengerjakan soal MTK ini JANGAN TELEDOR 

seperti misalnya diketahui di soal d = 28 ketika mengerjakan tidak dijadikan r dulu . inilah kesalahan yang fatal  

ok ini dia hasilnya.......            SEMOGA BERMANFAAT

A. BANGUN DATAR 

 

SPESIFIKASI

a. Persegi adalah bangun datar yang memiliki 4 sisi yang sama panjang.b. Mempunyai 4 sudut siku-siku 90⁰.
c. Mempunyai 2 diagonal yang sama panjang.

d. Mempunyai 4 simetri putar.  

e. Mempunyai 4 titik sudut.

RUMUS 

Rumus Luas Persegi

 L =    sisi   x   sisi

 Rumus Keliling Persegi

 K  =    4   x   sisi

B. PERSEGI PANJANG

   SPESIFIKASI

a. Persegi panjang merupakan bangun datar yang mempunyai 4 sisi.b. Mempunyai 4 sudut siku-siku 90⁰.
c. Mempunyai 2 diagonal yang sama panjang

d. Sisi yang berhadapan sama panjang dan sejajar.
e. Sisi-sisi persegi panjang saling tegak lurus
f.  Mempunyai 2 simetri putar

  RUMUS

Luas Persegi Panjang

 L =       p  x   l

Keliling Persegi Panjang

 K  =       2   x   ( panjang   +   lebar )

C. SEGITIGA

SPESIFIKASI

• Segitiga adalah bangun geometri yang dibentuk oleh 3 buah (sisi) dan membentuk 3 
• buah titik sudut 
• Jumlah sudut pada segitiga besarnya 180⁰ didapat dari penjumlahan 3 sudutnya.
• Bangun segitiga disimbolkan dengan ∆.

 RUMUS :

Luas Segitiga

 L =  alas x tinggi

      

                 2

Keliling segitiga

 K =  sisi 1  +  sisi 2 +   sisi 3 ( JUMLAH SELURUH SISI = AB+BC+CA ) 

D. JAJAR GENJANG

SPESIFIKASI 

a. Jajaran genjang merupakan bangun datar yang mempunyai 4 buah sisi.

b. Mempunyai 4 sudut, 2 sudut berpasangan dan berhadapan.

c. Sudut yang saling berdekatan besarnya 180⁰.

d. Mempunyai 2 diagonal yang tidak sama panjang.

e. Tidak mempunyai simetri lipat dan simetri putar.

f. Sisi yang berhadapan sejajar dan sama panjang.

g. Dua sisi lainnya tidak saling tegak lurus.

RUMUS : 

Keliling Jajaran Genjang
 

K  =       2   x   ( panjang   +   lebar )

 Luas Jajaran Genjang

L=       alas  x   tinggi

E. BELAH KETUPAT 

SPESIFIKASI :

a. Belah ketupat merupakan bangun geometri yang dibatasi 4 sisi sama panjang.

b. Mempunyai 2 diagonal yang berbeda panjangnya.

c. Mempunyai 4 titik sudut.

d. Sudut yang berhadapan besarnya sama.

e. Sisinya tidak tegak lurus.

f. Mempunyai 2 simeteri putar.

RUMUS :

 Luas Belah Ketupat

 L=  ½ x diagonal 1 x diagonal 2

 Keliling Belah Ketupat

 K =    4   x   sisi

F. LAYANG-LAYANG

SPESIFIKASI 

a. Layang-layang adalah bangun geometri berbentuk segiempat yang terbentuk dari dua segitiga  

b. sama kaki yang alasnya berhimpitan.

c. Mempunyai 4 sisi sepasang-sepasang yang sama panjang.

d. Mempunyai 4 buah sudut.

e. Sepasang sudut yang berhadapan sama besar.

f. Mempunyai 2 diagonal berbeda dan tegak lurus.

g. Tidak mempunyai simetri putar

RUMUS :

Luas Layang-Layang

L =     diagonal 1    x   diagonal 2                  
          

                                2

Keliling Layang-Layang

K  =    2  x  ( sisi panjang  +  sisi pendek )

G. TRAPESIUM

SPESIFIKASI 

Trapesium adalah bangun segiempat dengan sepasang sisi berhadapan sejajar.

Tiap pasang sudut yang sisinya sejajar adalah 180⁰.

Jenis-jenis trapesium :a.   Trapesium Siku-SIku          :  mempunyai sudut siku-siku.

b.    Trapesium Sama Kaki        :  mempunyai sepasang kaki sama panjanga.   

c.   Trapesium Sembarang        :  mempunyai sisi-sisi yang berbeda.

RUMUS 

KELILING TRAPESIUM

K = alas + sisi miring +  sisi miring + sisi atas

Luas Trapesium 

L =  (sisi atas + alas)  x   tinggi
      

                               2

SPESIFIKASI : 

Lingkaran merupakan kurva tertutup sederhana beraturan.

Jumlah derajat lingkaran sebesar 360⁰.

Lingkaran mempunyai 1 titik pusat.

Mempunyai simetri lipat dan simetri putar yang jumlahnya tidak terhingga.

Istilah-istilah dalam lingkaran :

• Diameter lingkaran (d) yaitu garis yang menghubungkan dua titik pada busur lingkaran melalui titik pusat lingkaran. d = 2. r
• Busur yaitu bagian lingkaran yang dibagi oleh tali busur.
• Juring yaitu daerah pada lingkaran yang dibatasi oleh 2 jari-jari maupun busur lingkaran. r = 1/2 d
• Sudut pusat yaitu sudut yang dibentuk oleh 2 buah jari-jari.

• Jari-jari lingkaran (r) yaitu ruas garis yang menghubungkan titik pada busur lingkaran dengan titik pusat lingkaran.

• Tali busur yaitu garis yang menghubungkan dua titik pada busur lingkaran dan tidak melewati titik pusat lingkaran.

  RUMUS :

Busur lingkaran

Panjang Busur AB  =  besar sudut AOB  X  keliling lingkaran  
                                

                                                                  360⁰

luas juring lingkaran

luas juring AOB  = sudut AOB X luas lingkaran ( jika diketahui sudut lain ( < COD X Luas linkrn)

                                

                                                 360⁰                                                                               < AOB

           

Luas Lingkaran

Luas   =   π   x   jari-jari  x  jari-jari

Luas   =   π  r2 (kuadrat)
       π  =   3,14 atau ( 22 )
                          

                                    7

        

Keliling lingkaran

K =   =  π  x diameter ATAU π x 2 x r           

             π  =  3,14 atau  ( 22 )
                                          7

sampai disini dulu ya..... SEMOGA BERMANFAAT 

jangan lupa guys kirim kan COMENT nya ya......

TETAP SEMANGAT karena MATEMATIKA gak sulit kok 

bye..... 

selanjutnya BANGUN RUANG

      A.  KUBUS

   SPESIFIKASI :

• Kubus merupakan bangun ruang dengan 6 sisi sama besar (kongruen)

• Kubus mempunyai 8 titik sudut.

• Jaring-Jaring kubus berupa 6 buah persegi yang SEBANGUN
• Kubus mempunyai 6 sisi berbentuk persegi.
• Kubus mempunyai 12 rusuk yang sama panjang.

RUMUS 

Luas Permukaan Kubus

L  =  6 x p x p atau p2 

L   :  luas permukaan
p   :  panjang rusuk

  

Rumus Volume Kubus

V  =  p x p x p atau p3 

V   :  Volume

p   :  panjang rusuk

B.  BALOK

• Balok mempunyai 6 sisi berbentuk persegi panjang.
• 4 buah rusuk yang sejajar sama panjang.
• Balok mempunyai 8 titik sudut.
• Balok mempunyai 3 pasang bidang sisi berhadapan yang kongruen.
• Balok mempunyai 12 rusuk.

RUMUS : 

LUAS PERMUKAAN BALOK

L  =  2 x [ (p x l) + (p x t) + (l x t) ]

L   :  luas permukaan
p   :  panjang balok
l    :  lebar balok
t    :  tinggi balok  

 Volume Balok 

V  =  p x l x t 

V   :  volume balok
p   :  panjang balok
l    :  lebar balok
t    :  tinggi balok

C. LIMAS

a - Limas adalah bangun ruang yang mempunyai bidang alas segi banyak atau n  dan dari bidang alas 

         tersebut dibentuk dari  suatu sisi berbentuk segitiga yang akan bertemu pada satu titik yang membentang keatas 

         b - Nama limas ditentukan oleh bentuk alasnya. misal  limas segi empat maka nama limas itu limas segi empat

c -Limas beraturan yaitu limas yang alasnya berupa segi beraturan.

d -  Tinggi limas adalah garis tegak lurus dari puncak limas ke alas limas

        
  Macam-macam bentuk limas :

a.    Limas segitiga          :  alasnya berbentuk segitiga

b.    Lima segiempat        :  alasnya berbentuk segi empat

c.    Limas segilima         :  alasnya berbentuk segilima

d.    Limas segienam       :  alasnya berbentuk segienam

rumus sederhana : limas segi  n

                                 

                                  2n buah rusuk, n+1 titik sudut dan sisi

RUMUS

LUAS PERUKAAN 

L = L alas + L sisi tegak  { lihat gambar }

Rumus Volume Limas

V =   ⅓  ( luas alas  x  t )

D. KERUCUT

                                           



Kerucut merupakan bangun ruang mirip seperti limas tetapi alasnya berupa 

lingkaran.

Kerucut mempunyai 1 titik sudut.

Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga.

Kerucut mempunyai 2 sisi.

Kerucut tidak  mempunyai rusuk.

rumus :

luas permukaan

  π x r x (r + s) 

  

volume kerucut

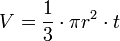
ket :  π = phi 22  atau 3,14

                   7

   r = jari jari  1 d

                             2

 s  = garis pelukis s =    √r2 + t2    

  t  = tinggi

E. LIMAS

                                 

• Prisma merupakan bangun ruang yang alas dan atasnya sebangun  dan sejajar..
• Prisma terdiri dari prisma segitiga dan prisma beraturan.
• Prisma segitiga mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen.
• Prisma segitiga mempunyai 5 sisi.
• Prisma segitiga mempunyai  9 rusuk
• Prisma segitiga mempunyai 6 titik sudut
• Jaring-jaring prisma segitiga berupa 2 segitiga, dan 3 persegi panjang.

Rumus sederhana : prisma segi n maka rusuk = 3 x n

                                                                          sisi    = n + 2

                                                                   titik sudut = 2 x n

 Luas Permukaan Prisma Segitiga

L  = 2 x luas alas + keliling alas x tinggi 

L   :  luas permukaan
∆   :  alas dan atas segitiga
t    :  tinggi prisma

  

Volume Prisma Segitiga

V  =  Luas Alas  x  t

V                     :  Volume
Luas Alas        :  Luas ∆   =  ( ½ a x t )
t                        :  tinggi prisma

F. TABUNG

a .Tabung merupakan bangun ruang berupa prisma tegak dengan bidang alas

    dan atas berupa  lingkaran.

b. Jaring-jaring tabung tabung berupa 2 buah lingkaran dan 1 persegi panjang.

c.Tinggi tabung adalah jarak titik pusat  lingkaran alas dengan titik pusat 

lingkaran atas.

d. Bidang tegak tabung berupa lengkungan yang disebut selimut tabung.

Rumus 

luas permukaan

volume

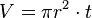  atau  v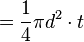  

G. BOLA 

                                    

a. Bola merupakan bangun ruang berbentuk setengah lingkaran

b. diputar mengelilingi garis tengahnya,.

c. Bola mempunyai 1 sisi dan 1 titik pusat.

d. Bola tidak mempunyai titik sudut dan rusuk

rumus 

luas  permukaan

bola utuh                      setengah bola padat              setengah bola berongga

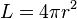                    3 π r2 (kuadrat)              2 x π x r2 (kuadrat)     

volume bola

bola utuh                      setengah bola padat              setengah bola berongga

4   π r3 (kubik)        2 x π x r3 (kubik)              2 x π x r3 (kubik)

3                                   3                                                3

SAMPAI SINI DULU YAA... SAYA KIRA UDH LENGKAP RUMUSNYA SEMOGA  

BERMANFAAT 

DAN DONT FORGET TO COMENT posting saya untuk evaluasi pembelajaran

byee..........

Demikianlah Artikel "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6

Sekian Kunci gitar "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan Chord gitar lagu kali ini.

Anda sedang membaca artikel "JAGOAN MATEMATIKA" KELAS 5 SD Sifat-Sifat Bangun dan Hubungan Antar Bangun BAB 6 dan artikel ini url permalinknya adalah http://arzulinux.blogspot.com/2016/04/matematika-kelas-5-sd-sifat-sifat.html Semoga artikel ini bisa bermanfaat.

Tweet